Tesis doctoral en indexación sobre espacios métricos

El pasado viernes 20 de Julio el profesor Dr Luis González Ares, miembro del Laboratorio de Bases de Datos de la Universidad de A Coruña, con quien nuestro grupo mantiene una estrecha colaboración, defendió la tesis doctoral titulada: «Métodos de Mejora de Rendimiento en Búsquedas por Similitud sobre Espacios Métricos». En esta tesis, dirigida por Óscar Pedreira y Nieves Rodríguez Brisaboa, se presenta por una parte un mecanismo de indexación denominado Índice de Pivote Único que supone una mejora bajo el criterio de ocupación de espacio del método de indexación Sparse Spatial Selection, desarrollado por Óscar Pedreira como punto central de su tesis doctoral y por otra parte una técnica denominada de «reducción de cluster» consistente en un particionado intra-cluster que reduce el número de puntos a evaluar dentro de cada cluster (bola de centro c y radio r).

La tesis, cuya escritura denota un gusto por el rigor científico y la precisión matemática por parte de su autor, se ubica en el marco de los índices métricos, esto es, estructuras de información que organizan el espacio métrico que componen los objetos de interés y las distancias entre ellos. Este tipo de índices explotan las propiedades de identidad, simetría y sobre todo desigualdad triangular de los espacios métricos con el objeto de minimizar el número de distancias que se necesitan calcular cuando se buscan puntos del espacio que estén cercanos a uno dado (bien porque sean vecinos próximos o bien porque se encuentren dentro de un rango determinado por una bola de centro c y radio r).

Los índices métricos están basados en la explotación de las propiedades de la distancia entre los objetos de una colección. A diferencia de otro tipo de métodos de acceso en espacios multidimensionales tales como B-trees (en el espacio unidimensional), k-d-trees, R-trees, Quad-trees, Grid-files, etc., que atienden generalmente a la localización de los datos dentro del espacio en que se ubican dichos objetos, los índices métricos utilizan las distancias entre los objetos de la colección para llevar a cabo una partición organizada del espacio que minimice el número de accesos que se precisan para responder a una determinada consulta. Normalmente este tipo de índices se utilizan para implementar consultas de vecindad, bien para localizar objetos que se encuentren en un rango determinado por un centro q (perteneciente al espacio de búsqueda) y un radio r (denominadas consultas por rango), o bien para localizar los vecinos más próximos a un punto dado q perteneciente al espacio de búsqueda (denominadas consultas del vecino más próximo «nearest neighbor query»).

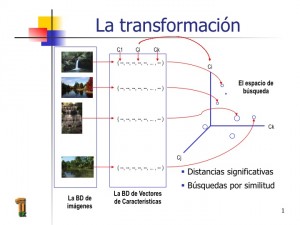
Este último tipo de consultas se utilizan con frecuencia en aplicaciones que precisan localizar objetos similares a uno dado. Por ejemplo en colecciones de imágenes, el usuario puede precisar localizar dentro de una colección aquellas imágenes que sean similares a una imagen determinada (proporcionada por el usuario). Para resolver este tipo de consultas, la imagen se convierte en un vector de valores que la caracterizan (utilizando por ejemplo descriptores como el color, la textura y la formas dentro de la imagen) y la similitud entre dos imágenes se puede implementar por medio de una función distancia que permita capturar la semejanza (o mejor dicho la falta de ella) entre los vectores que las caracterizan. De este modo, la colección de imágenes se transforma en un espacio métrico donde los objetos son puntos del espacio multidimensional definido por los vectores de características, dotado de una función distancia que mide la «disimilitud» entre cada dos puntos del espacio (mientras más cercanos están dos vectores, más semejantes son las imágenes que están caracterizando). Para efectuar una búsqueda de vecindad en un espacio métrico, el método más intuitivo consiste en calcular las distancias desde el punto de consulta q a todos los objetos de la colección y ofrecer como resultado el punto o los puntos a menor distancia de q (dependiendo de la consulta), pero es obvio que cuando la colección es grande, este método es claramente ineficiente. Es aquí donde los índices métricos pueden contribuir a mejorar los resultados. Si somos capaces de conocer a través de un índice que una zona del espacio métrico conteniendo una cantidad considerable de puntos, se encuentra a mayor distancia de un radio dado r donde focalizamos la búsqueda, es obvio que podemos descartar esa zona y ahorrarnos así el cálculo de muchas distancias entre el punto de consulta q y los puntos de esa zona.

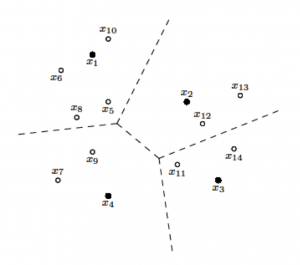
Para conseguir este objetivo, los índices métricos utilizan dos enfoques diferentes. El primero de ellos consiste en dividir el espacio en regiones (usualmente disjuntas), definidas por un determinado punto central y una colección de puntos alrededor de él. En esta clase se encuentran los índices basados en regiones de Voronoi (por ejemplo Voronoi tree), definidas por aquellos puntos que se encuentran más cerca del punto central que de cualquier otro punto central, o índices basados en bolas con un centro y un radio de cobertura, incluyendo todos los puntos que se encuentran a distancia menor o igual al radio de cobertura (por ejemplo el M-tree). Una búsqueda por rango con centro q y radio r en este tipo de índices permite descartar aquellas regiones del espacio cuya intersección con la bola de centro q y radio r es vacía. La propiedad de desigualdad triangular de la distancia permite descartar estas zonas sin necesidad de adentrarse en ellas para constatar su no relevancia.

El segundo de los enfoques consiste en seleccionar un número determinados de puntos del espacio, denominados pivotes, y para cada pivote, almacenar las distancias desde cada punto del espacio métrico a dicho pivote (por ejemplo el Vantage Point Tree o el propio Sparse Spatial Selection, diseñado e implementado por los directores de la tesis). Cuando se plantea una consulta de vecindad para un determinado punto q, se calculan las distancias entre el punto consulta q y el conjunto de pivotes de la colección. Utilizando entonces la desigualdad triangular y las distancias conocidas entre los puntos de la colección a cada pivote, se pueden ahorrar un número considerable de cálculos de distancia entre q y los puntos  del espacio. La tesis del Dr. Luis González propone la utilización del Índice de Pivote Único, cuyo objetivo es disminuir el número de distancias almacenadas para cada punto respecto del conjunto de pivotes seleccionados del espacio, reduciendo este número a un único pivote, precisamente aquel que mayores probabilidades tiene de evitar el cálculo de las distancias entre el punto de consulta q y un punto cualquiera del espacio de búsqueda. La disminución del número de distancias que debe almacenar el índice de pivote único consigue unos tamaños muy reducidos del índice que los hacen idóneos para casos en que las limitaciones de memoria son insoslayables  (por ejemplo para su utilización en smartphones) con unos rendimientos aceptables y competitivos en cuanto a tiempo de respuesta de las consultas.

Desde aquí mi felicitación a su autor y a los directores de esta tesis doctoral, la cual además de constituir una interesante contribución investigadora en el campo de los índices métricos, nos provee de un magnífico material académico de fácil lectura para entender la problemática subyacente en la indexación de espacios métricos. La memoria puede descargarse desde la página web de su autor.